Trains have been the fundamental backbone of transportation and shipping for a few hundred years. Despite the ubiquity of trains, the details of their workings are a bit of a mystery. Trains have come about as more of a feat of engineering than one of science. Thus, the detailed scientific theory of trains has remained aloof. There are some common unknowns with trains. For example, if you’ve watched a race on a round track before, you notice that lanes that go around a curve are different distances. That is because the distances on the inside and the outside of the track are different. This principle obviously holds for trains too, then why is it that a train can turn on the tracks?
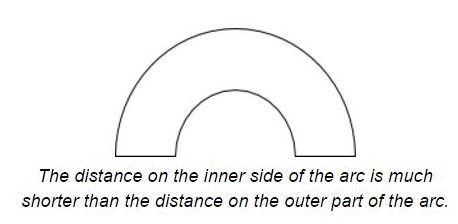
Source: Sciworthy Original
The inner versus outer track distances is actually solved because trains of conical wheels. These conical wheels can allow the train to slide sideways slightly to make up for the difference in distances between the two tracks. Thus, trains stay axled, with the wheels on both sides of the train rotating at the same speed, and are still able to go around curves. When trains go around curves and corners, they must tilt.
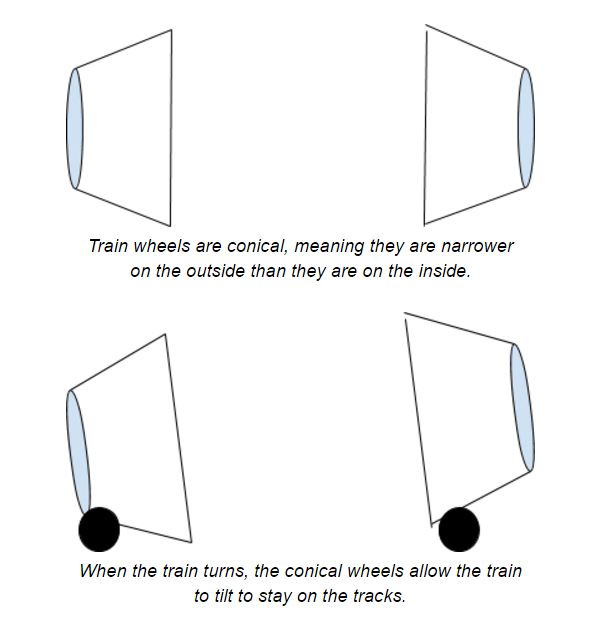
Source: Sciworthy Original
With all this tilting, it’s surprising that trains don’t fall over. Even moreso, the wheels of a train are small compared to the height, speeds, and momentum of trains. Then why do minor bumps and wobbles not derail these kilometer-long trains? A shifting load or snow on the tracks does not even bother these trains and they always end up being stable, even on a curve!
A scientist, Dr. Shayak set out to determine mathematically WHY trains do stay on their tracks. The physics of trains is complex and there are many moving parts to consider. Thus, to do the in-depth analysis of trains, many assumptions had to be made to break down the problem.
First, a single axle system was assumed, therefore the left and right side of the train wheels turn together. Secondly, a train works optimally when it does not slip or jump, so only smooth rolling was assumed. Lastly, the trains were assumed to be well balanced. Trains can be loaded in a variety of ways. This heavily adjusts the balancing physics of the trains. Dr. Shayak used these assumptions to derive the moment of inertia tensor of a train. A “moment of inertia tensor” is a mathematical tool used in physics to determine the stability of a physical object.
Dr. Shayak found the reason these trains never tip is also because of their conical wheels. The conical wheels’ shape, every time the train tips, the amount that it tips acts to restore the train upright. This force, called a restoring force, is stronger when the train is heavier meaning heavier trains are more stable.
This precise, physical description allowed Dr. Shayak to find exactly what wheel angle was the most stable. This angle was found to be 2.86 degrees. Coincidentally, this is the angle that many imperial trains in Britain and India use for their wheels!
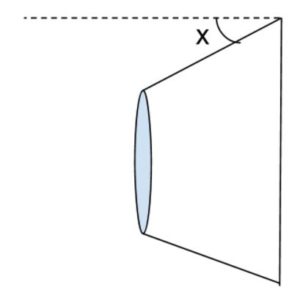
The angle, X, that was optimized in the present study. Source: Sciworthy Original
This scientific contribution doesn’t tell us anything we didn’t already know. We know that trains run reliably. Also, the derived optimal angle scientifically had already been considered. This paper is a major contribution because it unveiled a very simple, clear, and elegant analysis of trains. This clear communication demystified many of the unknowns about trains, and broke down a very difficult problem into a tangible, well analysed problem. This revolutionary analysis allows this problem to be used as a teaching tool for introductory physics classes! Even studying solved problems is useful to the field, as sometimes scientists discover a new simple solution to a complex problem.


